Multisig vs MPC: Understand the key differences between these two crypto wallet security methods.

MPC vs Multisig: What’s the Difference?

Reading Time: 8 minutes

As crypto adoption accelerates, so does the need for secure, flexible ways to manage digital assets. Two popular technologies – Multisignature (Multisig) and Multi-Party Computation (MPC) – are often brought up when discussing wallet security and access control. But what do they actually mean? How do they work? And which one is right for your business?

If you’re not deeply technical, don’t worry – in this post, we’ll break down the difference using simple analogies, visuals, and practical examples.

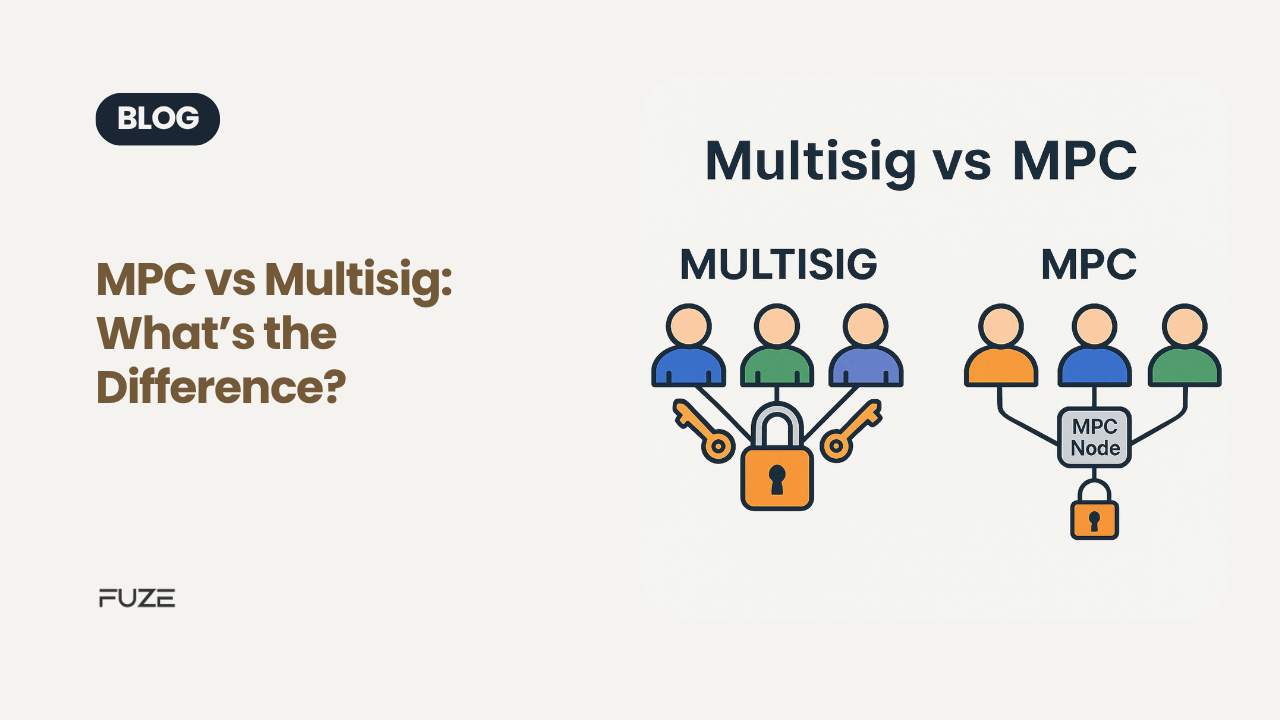
A Vault Full of Gold

Let’s start with a relatable analogy.

Imagine you and a few partners store gold in a high-security vault. To prevent fraud or theft, you don’t want any one person to open the vault alone. You need a system of shared control.

There are two ways to set this up:

Option 1: Multisig (Multisignature): Like putting multiple locks on the vault

  • The vault has 5 locks.

  • Each of your 5 partners has a unique key.

  • You configure the vault to require at least 3 of those 5 keys to open it.

This is how Multisig works on blockchains like Bitcoin or Ethereum (via smart contracts). It’s a rules-based setup, where a minimum number of authorized parties must individually approve a transaction.

Pros:

  • Simple and battle-tested.

  • Transparent – everyone can see on the blockchain that multiple approvals were required.

  • Useful for shared wallets (e.g., company treasuries, DAOs).

Cons:

  • Limited flexibility – changing participants or rules requires on-chain updates.

  • Privacy is poor – the multisig setup and signers are visible to everyone.

  • Implementation differs across blockchains – not all chains support the same features.

Option 2: MPC (Multi-Party Computation): Like sharing pieces of a single secret key – invisible cooperation

Now imagine:

  • The vault has just one lock.

  • But instead of giving the full key to one person, you split it into secret pieces.

  • Each person holds a piece, and when needed, they work together to generate a valid key without ever assembling it in one place.

That’s MPC in action – it uses advanced cryptography so that multiple parties can collaboratively “sign” a transaction, without revealing or reconstructing the private key.

From the outside, it looks like just one person signed – even though multiple people participated behind the scenes.

Pros:

  • Chain-agnostic – works on any blockchain that supports regular signatures (e.g., Bitcoin, Ethereum, Solana).

  • Private – no one knows multiple parties were involved.

  • Flexible – easy to rotate participants, revoke access, or add devices.

  • Great for mobile wallets, institutions, and any system needing seamless security.

Cons:

  • Complex to implement – requires sophisticated infrastructure.

  • Harder to audit – no visible “multi-party” footprint on-chain.

  • Often depends on off-chain coordination or vendors.

Why the Confusion?

MPC and Multisig both aim to reduce single points of failure – meaning, they protect against the risk of one person or device being compromised. But they do so in very different ways.

Multisig is visible and rule-based, great for open accountability.
MPC is invisible and cryptographic, perfect for security with minimal friction.

You’ll often see them compared, debated, or even combined in some enterprise-grade solutions.

Architectural Differences

Multisig Wallet Architecture

  • Each participant holds a full key.

  • Wallet logic is enforced on-chain (Bitcoin script, Ethereum contract).

  • Transactions show multiple signers.

┌────────────┐
│ Alice Key  │
└─────┬──────┘
      │
┌─────▼─────┐
│ Wallet    │ ← Logic: 2-of-3 enforced on-chain
└─────▲─────┘
      │
┌─────┴─────┐
│ Bob Key   │
└───────────┘

MPC Wallet Architecture

  • One private key is split across N parties.

  • Signing happens off-chain, cooperatively.

  • On-chain, it appears like a standard signature.

┌────────────┐
│ Share A    │
└────┬───────┘
     │
┌────▼──────┐
│ MPC Node  │
└────┬──────┘
     │ Shares never combined!
┌────▼───────┐
│ Share B    │
└────────────┘

A Technical Deep Dive: Comparing Multisig and MPC in Python

If you’ve made it this far, you’re probably curious to see how these concepts play out in actual code.

Below, we’ll walk through simplified Python snippets that demonstrate the core principles behind Multisignature (Multisig) and Multi-Party Computation (MPC) wallet mechanisms.

⚠️ Disclaimer:
This code is intentionally simplified for educational purposes. It is not production-grade and doesn’t represent the cryptographic depth or infrastructure required in real-world blockchain environments like Bitcoin or Ethereum. Real implementations involve secure key storage, cryptographic libraries, hardware modules, threshold schemes, and network coordination.

With that out of the way, let’s dig in.

Multisig example

# prerequisite: pip3 install ecdsa

from ecdsa import SigningKey, VerifyingKey, SECP256k1, BadSignatureError
import hashlib
import random

# === 1. Generate 3 ECDSA key pairs ===
keys = [SigningKey.generate(curve=SECP256k1) for _ in range(3)]
pubkeys = [key.verifying_key for key in keys]

print("🔐 Generated 3 key pairs")

# === 2. Message to sign ===
message = b"This is an academic multisig demo"
message_hash = hashlib.sha256(message).digest()

# === 3. Randomly pick any 2 signers ===
signer_indices = random.sample([0, 1, 2], 2)
signatures = [keys[i].sign(message_hash) for i in signer_indices]

print(f"\n🖋️ Signers: {signer_indices}")

# === 4. Verification logic ===
def verify_multisig(message_hash, signatures, pubkeys, threshold=2):
valid_count = 0
for sig in signatures:
for pub in pubkeys:
try:
if pub.verify(sig, message_hash):
valid_count += 1
break # Avoid double-counting same signature
except BadSignatureError:
continue
return valid_count >= threshold

# === 5. Result ===
is_valid = verify_multisig(message_hash, signatures, pubkeys, threshold=2)
print("\n✅ Multisig verification result:", is_valid)

Let’s break down the code step-by-step:

1. Key Generation

# === 1. Generate 3 ECDSA key pairs ===
keys = [SigningKey.generate(curve=SECP256k1) for _ in range(3)]
pubkeys = [key.verifying_key for key in keys]
  • The script starts by creating three distinct ECDSA key pairs. Each pair consists of a private key (for signing) and a corresponding public key (for verification).
  • keys stores the three private SigningKey objects.
  • pubkeys stores the three public VerifyingKey objects.
  • This setup represents a group of three parties who can authorize a transaction.

2. Message Hashing

# === 2. Message to sign ===
message = b"This is an academic multisig demo"
message_hash = hashlib.sha256(message).digest()
  • A message is defined. In a real-world scenario, this would be the details of a transaction.
  • The message is then hashed using the SHA-256 algorithm. It’s standard practice to sign the hash of the message rather than the full message for efficiency and security.

3. Signing

# === 3. Randomly pick any 2 signers ===
signer_indices = random.sample([0, 1, 2], 2)
signatures = [keys[i].sign(message_hash) for i in signer_indices]
  • To simulate a 2-of-3 multisig, the script randomly selects two of the three key pairs to act as signers.
  • Each of the two selected signers uses their private key (keys[i]) to sign the message_hash.
  • The result is a list containing two digital signatures.

4. Verification Logic

# === 4. Verification logic ===
def verify_multisig(message_hash, signatures, pubkeys, threshold=2):
    valid_count = 0
    for sig in signatures:
        for pub in pubkeys:
            try:
                if pub.verify(sig, message_hash):
                    valid_count += 1
                    break
            except BadSignatureError:
                continue
    return valid_count >= threshold
  • This is the core of the multisig verification.
  • The function takes the message hash, the list of signatures, the list of all three public keys, and a threshold (the minimum number of valid signatures required).
  • It iterates through each provided signature. For each signature, it then iterates through all the public keys in the authorized group.
  • pub.verify(sig, message_hash) checks if a given signature is valid for a specific public key. If it is, valid_count is incremented, and the inner loop breaks to check the next signature.
  • If verify fails (which is expected when trying a signature against the wrong public key), it raises a BadSignatureError, which is caught and ignored.
  • Finally, the function returns True only if the number of valid signatures meets or exceeds the required threshold.

5. Result

# === 5. Result ===
is_valid = verify_multisig(message_hash, signatures, pubkeys, threshold=2)
print("\n✅ Multisig verification result:", is_valid)
  • The script calls the verify_multisig function with the generated data.
  • Since two valid signatures were created and the threshold is two, the verification will succeed, and the script will print True.

In essence, this script effectively models a scenario where an action requires approval from at least two out of three designated individuals before it can be considered valid. To see the failure in action, you could have only 1 signer in signer_indices and see it fail!

MPC example

import hashlib
import secrets
from ecdsa import SECP256k1, SigningKey, VerifyingKey
from ecdsa.util import number_to_string, string_to_number, sigencode_string, sigdecode_string

curve = SECP256k1
G = curve.generator
n = curve.order

def sha256(msg: str) -> int:
return int(hashlib.sha256(msg.encode()).hexdigest(), 16)

def modinv(a: int, n: int) -> int:
return pow(a, -1, n)

def generate_key_share():
return secrets.randbelow(n)

# === 1. Key generation (additive shares) ===
sk_A = generate_key_share()
sk_B = generate_key_share()
sk = (sk_A + sk_B) % n
pk = sk * G

print("🔐 Private shares:")
print("sk_A:", hex(sk_A))
print("sk_B:", hex(sk_B))
print("Combined sk:", hex(sk))
print("\n🪪 Public key:", (pk.x(), pk.y()))

# === 2. Message and ephemeral key ===
message = "Hello from MPC world"
z = sha256(message)
k = generate_key_share()
R = k * G
r = R.x() % n
k_inv = modinv(k, n)

# Each party computes r * sk_i
rA = (r * sk_A) % n
rB = (r * sk_B) % n
r_sum = (rA + rB) % n

# === 3. Compute signature s ===
s = (k_inv * (z + r_sum)) % n
print("\n📜 Signature:")
print("r:", hex(r))
print("s:", hex(s))

# === 4. Verify using ecdsa library ===
# Convert public key to VerifyingKey object
vk = VerifyingKey.from_public_point(pk, curve=SECP256k1)

# Encode r and s into byte format expected by ecdsa
r_bytes = number_to_string(r, n)
s_bytes = number_to_string(s, n)
signature = r_bytes + s_bytes

valid = vk.verify(signature, message.encode(), hashfunc=hashlib.sha256, sigdecode=sigdecode_string)
print("\n✅ Signature valid?", valid)

Let’s break it down section by section.

1. Setup and Helper Functions

  • Imports: It imports standard libraries like hashlib for hashing and secrets for generating cryptographically secure random numbers. The core logic relies on the ecdsa library for elliptic curve operations.
  • Curve Parameters: It defines the SECP256k1 curve, which is the same one used by Bitcoin and Ethereum. G is the generator point of the curve, and n is the order of the curve’s base point, a large prime number that defines the finite field for our calculations.
  • Helper Functions:
    • sha256(msg): A simple function to compute the SHA-256 hash of a message.
    • modinv(a, n): Calculates the modular multiplicative inverse of a modulo n, which is crucial for the signature calculation.
    • generate_key_share(): Creates a secure random number smaller than n, which will serve as a piece of the private key.

2. Key Generation (The MPC Part)

This is where the “multi-party” concept begins. Instead of a single entity creating and holding a private key, the key is split into shares.

  • Private Key Shares: Two shares, sk_A and sk_B, are generated. You can think of these as belonging to two different people or devices, Alice and Bob.
  • Combined Private Key: The full private key sk is the sum of these shares (sk_A + sk_B) modulo n. Crucially, in a real MPC system, the combined sk is never actually calculated or held by any single party. They only know their own share.
  • Public Key: The public key pk is derived from the combined private key (pk = sk * G). This can also be computed without ever combining the private shares. Alice computes her public share (pk_A = sk_A * G), Bob computes his (pk_B = sk_B * G), and they can combine these to get the final public key (pk = pk_A + pk_B).

3. Signature Generation (The Collaborative Part)

This section demonstrates how Alice and Bob can work together to sign a message without revealing their private key shares.

The standard ECDSA signature (r, s) is calculated as:

  • r = (k * G).x() % n
  • s = k⁻¹ * (z + r * sk) % n

Where k is a temporary secret number and z is the message hash.

Here’s how it’s done collaboratively in the script:

  1. Message and Ephemeral Key: A message is chosen, and its hash z is computed. A one-time secret k is generated.
  2. Calculate r: r is calculated from k and the generator point G. This value is public and forms the first part of the signature.
  3. Collaborative Calculation: The term r * sk is needed to compute s. Since neither party has the full sk, they compute their part of it:
    • Alice computes rA = (r * sk_A) % n.
    • Bob computes rB = (r * sk_B) % n.
    • They then sum these partial results: r_sum = (rA + rB) % n. This r_sum is mathematically equivalent to (r * sk) % n.
  4. Compute s: With r_sum calculated, either party can now compute the final s value, the second part of the signature.

4. Verification

This final step is standard for any ECDSA signature. Anyone with the public key pk can verify that the signature (r, s) is valid for the given message. The script uses the ecdsa library to perform this verification, confirming that the collaboratively generated signature is indeed correct.

In essence, this script elegantly demonstrates the core principle of MPC for signatures: splitting a secret (the private key) into shares and then using a protocol to perform computations with that secret without ever bringing the shares together in one place. You could simulate the error scenario by making a small change where in the collaborative part, one of the parties does not contribute to creating their part of the signature!

Conclusion

While both approaches aim to eliminate single points of failure and improve wallet security, they differ greatly in architecture and user experience. Multisig is easier to understand and audit, while MPC provides a seamless, private, and flexible foundation, especially useful in mobile and enterprise-grade wallets.

Whether you lean toward multisig’s transparency or MPC’s stealthy coordination, understanding both is key to building (or choosing) a secure crypto wallet system.

At Fuze, we’re deep in the weeds of crypto infrastructure so you don’t have to be. From abstract concepts to real-world deployment, we keep up with the latest tech – thoughtfully, securely, and always with user experience in mind! ✨

Tags: , , ,